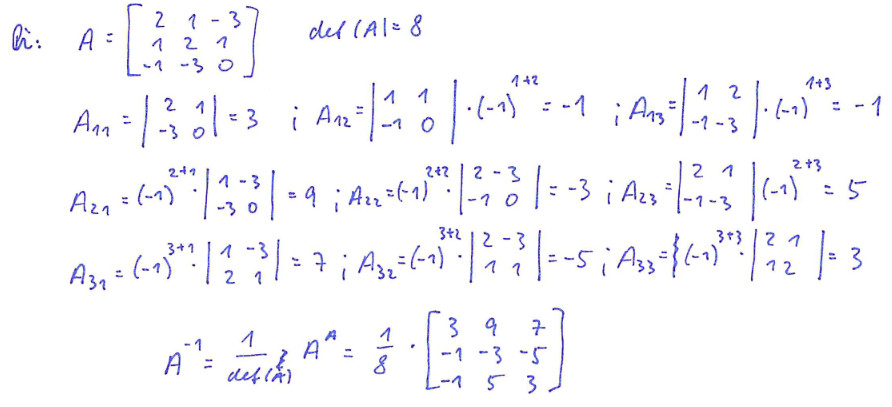FAV-ZCU/KMA LAA/5. Hodnost matice.md

Hodnost matice

• počet nenulových řádků matice

Řádkový a sloupcový prostor matice

U matice A typu m/n je

• lineární obal všech řádkových vektorů (řádků) nazýván řádkovým prostorem matice A;
• lineární obal všech sloupcových vektorů (sloupců) nazýván sloupcovým prostorem matice A.

Dimenzi řádkového nebo sloupcového prostoru nazveme řádkovou (sloupcovou) hodností matice A a značíme ji hod^r(A) resp. hod^s(A).

A = \begin{bmatrix}
1 & 2 & 5 \\
-2 & 3 & -4 \\
-1 & 5 & 1
\end{bmatrix} \space \begin{matrix}
\leftarrow r_{1} \\
\leftarrow r_{2} \\
\leftarrow r_{3}
\end{matrix}

M = \biggl\{ \begin{bmatrix}
1 \\
2 \\
5
\end{bmatrix}; \begin{bmatrix}
-2 \\
3 \\
-4
\end{bmatrix}; \begin{bmatrix}
-1 \\
5 \\
1
\end{bmatrix} \biggl\}

• M generuje řádkový lineárně vektorový prostor matice A.
• M je LZ, neboť r_3^T = r_1^T + r_2^T, tedy dim(M) < 3.
• Ale \{r_1^T, r_2^T\} je LN a tedy báze, proto hod^R(A) = 2.

Pro každou matici A platí, že

• řádková hodnost je rovna té sloupcové, takže hod^r(A) = hod^s(A);
• hodnost transponované matice je rovna hodnosti původní matice, takže hod(A) = hod(A^T).

Hodností matice A nazveme hodnotu hod^r(A).

Regulární matice

vlastnost	výraz
její hodnost se rovná jejímu řádu	hod(A) = n
má nenulový determinant	\det{A} \neq 0
existuje k ní inverzní matice	\text{existuje } A^{-1}

Každou regulární matici lze řádkovými elementárními úpravami převést na jednotkovou matici.

Singulární matice

vlastnost	výraz
její hodnost je menší než její řád	hod(A) < n
má nulový determinant	\det{A} = 0
neexistuje k ní inverzní matice	\text{neexistuje } A^{-1}

Určení hodnosti pomocí determinantu

Determinant trojúhelníkové matice je roven součinu prvků na hlavní diagonále.

Determinant libovolné čtvercové podmatice řádu m se nazývá minorem řádu m matice A.

Hodnost matice A je rovna rozměru největšího nenulového subdeterminantu.

Nechť A je matice. Potom je hod(A) = m právě tehdy,

• když v A existuje nenulový minor řádu m
• a zároveň každý minor řádu většího než m je nulový.

Nechť A je čtvercová řádu n. Potom hod(A) = n, pokud se \det(A) nerová 0.

• DK: Podle předchozí věty je hod(A) = n \iff v A existuje nenulový minor řádu n.
• Víme, že jedinému minoru řádu n odpovídá celá matice A, tedy hod(A) = n \iff \det(A) se nerovná 0.

Inverzní matice

Inverzní matice A^{-1} nemusí pro matici A vždy existovat. Pokud ale existuje, je jednoznačně určená.

• A \cdot A^{-1} = A^{-1} \cdot A = I
• (AB)^{-1} = A^{-1}B^{-1}

Inverzní matice A^{-1} k matici A existuje pouze, pokud je matice A regulární.

Adjungovaná matice

Adjungovaná matice je matice A^A, která je poskládaná z algebraických doplňků, ale transponovaně.

Určení inverzní matice pomocí determinantů

Pokud je matice A regulární, je možné získat inverzní matici.

\displaystyle A^{-1} = \frac{1}{\det(A)} \cdot A^A

!