1.4 KiB
1.4 KiB
Ekvivalence a rozklad množiny
Ekvivalence
Ekvivalence na množině X je relace R na množině X, která je reflexivní, symetrická a tranzitivní.
Třídy rozkladu
Nechť X a I jsou množiny. (Neuspořádaný) soubor podmnožin X_{i}: i \in I množiny X je rozklad množiny X, pokud množiny X_{i} jsou neprázdné, navzájem disjunktní (nemají společné prvky) a jejich sjednocením je celá množina X. Množiny X_{i} nazýváme třídy rozkladu X_{i}: i \in I.
- soubor podmnožin = rozklad množiny
- jednotlivé množiny = třídy rozkladu
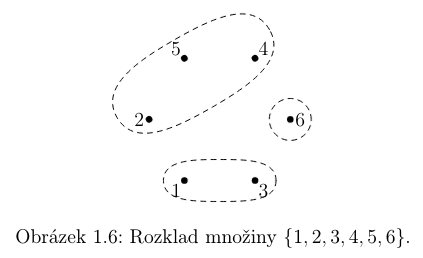
Soubor S = \{\{1, 3\}, \{6\}, \{2, 4, 5\}\}, je například rozkladem množiny X = \{1, 2, 3, 4, 5, 6\}, zatímco soubory \{\{1, 2, 3\}, \{1, 4, 5\}, \{1, 5, 6\}\} a \{\{1, 2\}, \{3, 4, 5\}\} nikoli. V rozkladu nezáleží na pořadí tříd.
Třídy ekvivalence
Je-li \sim ekvivalence, pak se třídy příslušného rozkladu nazývají třídy ekvivalence \sim.
- Pokud je relace ekvivalencí, třídy rozkladu nazveme třídami ekvivalence.
Stirlingova čísla
Počet rozkladů n-prvkové množiny
- počet prvků rozkladu
k - počet všech takových rozkladů?
S(n, k) \qquad |x| = nk = n \qquad S(n,n) = 1, S(n,1) = 1S(n,k) = S(n-1,k-1) + k\cdot S(n-1,k), z \in X- Stirlingova čísla (2. druhu)