Výpočetní složitost

doba výpočtu T(n) v závislosti na vstupu n
- je důležité určit, co je důležité
- zajímá nás, co se děje, když n roste
- různé funkce rostou různě rychle
druhy algoritmů
- rychle rostoucí funkce = neefektivní algoritmus
- pomalu rostoucí funkce = efektivní algoritmus
záleží na tom, jestli se funkce vejde pod jinou
- například lineární pod kubickou
- ne hned, ale od nějakého n_0 ano
- nezáleží na násobku, jen to n_{0} bude dál

O-notace

O(f(n)) je množina všech funkcí, pro které platí, že g(n) < c \cdot f(n) pro všechna n > n_0 > 0 a nějaké c > 0.

je-li g(n) \in O(f(n)), pak
- g(n) se vejde pod f(n)
- g(n) neroste rychleji než f(n)

Význam O-notace:

omezuje funkci jen shora
je záruka (nebude to horší než...)
příslušnost do O(f(n)) implikuje efektivitu, pokud f(n) roste dost pomalu

U funkcí nezáleží na přenásobení konstantou, přičtení konstanty ani na základu logaritmu:

pokud	platí také
`g(n) \in O(kf(n))`	`g(n) \in O(f(n))`
`g(n) \in O(k + f(n))`	`g(n) \in O(f(n))`
`O(\log_{a}(n)) =`	`O(\log_{b}(n))`

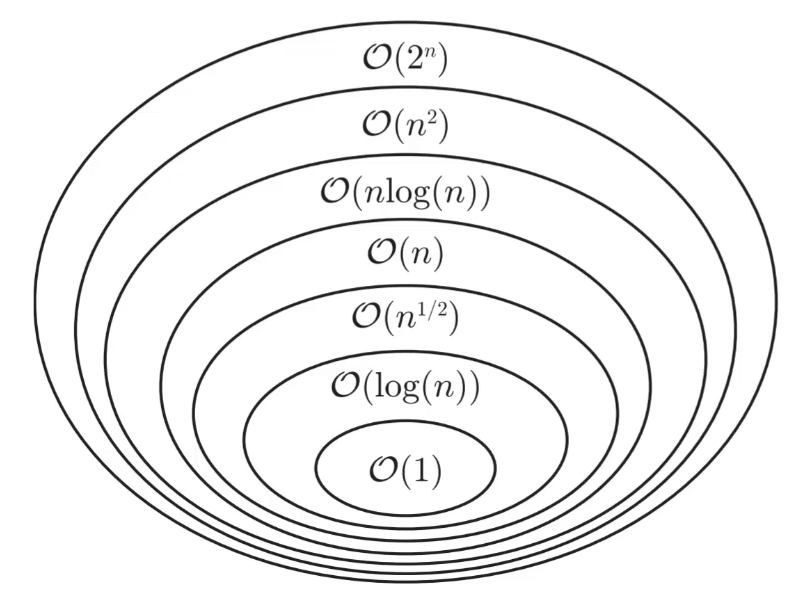
Mezi některými množinami O(f(n)) platí tyto vztahy:

$$ O(1) \subset O(\log(n)) \subset O(\sqrt{n}) \subset 0(n) \subset O(n \cdot \log(n)) \subset O(n^2) \subset O(n^3) \subset O(2^n) \subset 0(e^n)

U 0-notace nezáleží na násobku ani na přičtení konstanty či menší funkce, proto se např. g(n) = 2 \cdot n^2 + 5 \cdot n + 4 vejde pod 0(n^2).

Omega notace

\Omega(f(n)) je množina všech funkcí, pro které platí, že g(n) > c \cdot f(n) pro všechna n > n_0 > 0 a nějaké c > 0. (jediná změna je ve znaménku větší než)

Omega notace je opakem O-notace
funkce g(n) patří do \Omega(f(n)) když g(n) roste stejně rychle nebo rychleji než f(n)

Význam Omega notace:

omezuje funkci jen zdola
říká, že to nebude lepší než...
příslušnost do \Omega(f(n)) implikuje neefektivitu, pokud f(n) roste rychle

Mezi Omega množinami existují obrácené vztahy oproti O-množinám.

Theta notace

Pokud g(n) \in O(f(n)) a zároveň g(n) \in \Omega(f(n)), pak g(n) \in \Theta(f(n)).

neroste rychleji ani pomaleji - roste stejně rychle
graf g(n) je od jistého n_{0} možné uzavřít mezi grafy c_{1} \cdot f(n) a c_{2} \cdot f(n)
- patrně c_{1} < c_{2}

Theta množiny jsou disjunktní - funkce nemůže patřit do více množin zároveň.

Výjimka: Pokud g_{1}(n) = 1000n, g_{2}(n) = n\log(n), pak pro všechna realistická n platí g_{2}(n) < g_{1}(n), protože funkce g_{1} bude efektivnější až ve velmi velkých číslech.

Důležitá poznámka

Význam funkcí může být:

čas výpočtu pro jakýkoli vstup velikosti n
čas výpočtu pro nejlepší možný vstup velikosti n
čas výpočtu pro nejhorší možný vstup velikosti n
průměrný čas výpočtu pro vstup velikosti n
počet instrukcí pro ...
množství paměti nutné pro zpracování ...
...

Je ale potřeba nesrovnávat hrušky s pomeranči.

Jeden program může mít v očekávaném případě lepší efektivitu než jiný v tom nejhorším případě, přesto však ten první nemusí být lepší (v nejhorším případě může být mnohem méně efektivní).

Určení výpočetní složitosti programu

je potřeba určit funkci g(n)
při určování můžeme zanedbat časy jednotlivých instrukcí, pokud jsou opravdu konstatní (nezávislá na parametru n)
výpočetní složitost neřeší rozdílné výkony počítačů

3.7 KiB Raw Blame History