FAV-ZCU/KMA DMA/Otázky ke zkoušce/17. Souvislost orientovaného grafu.md

Souvislost orientovaného grafu

Pojmy podgraf a indukovaný podgraf jsou definovány stejně jako u neorientovaných grafů.

Symetrizace orientovaného grafu

Symetrizací orientovaného grafu \vec{G} nazveme neorientovaný graf G, kde V(G) = V(\vec{G}) a E(G) = \left\{ \{ x, y \}; (x, y) \in E(\vec{G}) \right\}.

Z orientovaného grafu můžeme snadno vyrobit neorientovaný graf tím, že "zapomeneme" orientaci všech hran. Případné smyčky odstraníme a násobné hrany nahradíme jednoduchými.

Orientace neorientovaného grafu

Orientací neorientovaného grafu G nazveme orientovaný graf \vec{G} s V(\vec{G}) = V(G) a pro každou hranu e \in E(G) zvolíme v \vec{G} jednu ze dvou možných orientací.

Symetrickou orientací neorientovaného grafu G nazveme graf \vec{G}_{s} takový, že V(\vec{G}_{s}) = V(G) a E(\vec{G}_{s}) = \left\{ (x, y), (y, x); \{ x, y \} \in E(G) \right\}.

• vrcholy jsou stejné a hrany tohoto grafu jsou obousměrné (oběma směry)

Okolí a stupně orientovaných grafů

Mějme orientovaný graf \vec{G} a vrchol v \in V(\vec{G}).

Vstupním okolím vrcholu x v \vec{G} nazveme vrcholy N^\text{in}(x) = \left\{ v \in V(\vec{G}) ; (v, x) \in H(\vec{G}) \right\}.

Výstupním okolím vrcholu x v \vec{G} nazveme vrcholy N^\text{out}(x) = \left\{ v \in V(\vec{G}) ; (x, v) \in H(\vec{G}) \right\}.

Vstupním stupněm vrcholu x nazveme číslo d^\text{in}(x) = \vert N^\text{in}(x) \vert.

Výstupním stupněm vrcholu x nazveme číslo d^\text{out}(x) = \vert N^\text{out}(x) \vert.

Nechť \vec{G} je orientovaný graf, potom

• \displaystyle\sum_{v \in V(\vec{G})} d^\text{in}(v) = \sum_{v \in V(\vec{G})} d^\text{out}(v) = m.
• V grafu je stejný počet vstupních hran jako výstupních (jen jsou u jiných vrcholů) a tvoří všechny hrany daného grafu.

Slabá souvislost

Řekneme, že orientovaný graf \vec{G} je (slabě) souvislý, je-li jeho symetrizace G souvislý graf.

Silná souvislost

Pro orientované grafy lze snadno upravit definice sledů, cest a kružnicí v grafu.

Orientovaný sled z vrcholu x do vrcholu y v orientovaném grafu $\vec{G}$ je posloupnost vrcholů (x = v_{0}, v_{1}, \dots, v_{k} = y), ve které je pro každé $i = 1, \dots, k$ dvojice v_{i−1}v_{i} hranou grafu \vec{G}.

Orientovaná cesta v \vec{G} je orientovaný sled, který obsahuje každý vrchol nejvýše jednou.

Orientovaný graf \vec{G} je silně souvislý, pokud v něm pro každou dvojici vrcholů x, y existuje orientovaná cesta z x do y i orientovaná cesta z y do x.

Cyklus

Cyklus v \vec{G} je orientovaný sled, ve kterém je v_{0} = v_{k}, tento vrchol je v něm obsažen právě dvakrát a všechny ostatní nejvýše jednou.

Graf \vec{G} je silně souvislý právě tehdy, pokud je jeho každá hrana obsažena v nějakém cyklu.

Graf \vec{G} je acyklický, jestliže \vec{G} neobsahuje jako podgraf žádný cyklus.

Relace oboustranné dosažitelnosti

Nechť G je orientovaným grafem. Potom na vrcholech x, y \in V(G) definujeme relaci oboustranné dosažitelnosti x \sim y, pokud v G existuje orientovaná cesta z x do y i naopak.

• tato relace je
  • reflexivní
  • symetrická
  • tranzitivní - x \sim y \wedge y \sim z \implies x \sim z
  • je to ekvivalence
• \implies rozklad V(G) na třídy ekvivalence

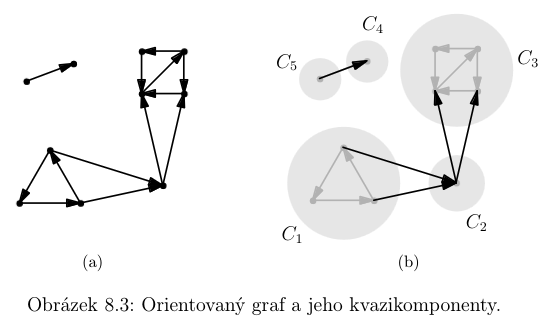
Kvazikomponentou (silnou komponentou) nazveme maximální silně souvislý podgraf grafu \vec{G}.

• jedná se o podgraf indukovaný na třídě ekvivalence
• dvě různé kvazikomponenty \vec{G} nemají společný vrchol

!

Kondenzace

Kondenzace orientovaného grafu G je orientovaný graf G_{c}, jehož vrcholy jsou kvazikomponenty grafu G, a pro různé kvazikomponenty Q_{1}, Q_{2} \in V(G_{c}) platí:

• Q_{1}Q_{2} \in E(G_{c}), pokud pro nějaké x_{1} \in V(Q_{1}), x_{2} \in V(Q_{2}) je x_{1}x_{2} \in E(G).